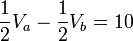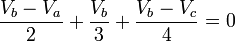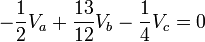DEFINICIÓN DE NODO
Si tenemos un punto en el cual se conectan dos o más ramas eléctricas y por el cual fluyen distintas corriente eléctricas, entonces podemos denominar este punto como un Nodo o también llamada nudo, este punto es un empalme de conductores formados por alambres ideales (despreciando su resistencia).
Si en la Terminal
A se empieza el recorrido alrededor del circuito, pasando en orden por cada nodo
(a, b, c, d); entonces habremos recorrido una trayectoria cerrada por nodos. Desde este punto de vista la ley de las corrientes de
kirchhoff nos dice que la suma algebraica de las corrientes en un nodo es cero
0 en todo instante, por lo que una carga

no puede acumularse en un nodo.
RESOLUCIÓN POR NODOS
1. elegimos los nodos a los cuales les calcularemos la corriente que entra y sale de este punto
(Va, Vb, Vc, Vd) teniendo en cuenta que uno de estos nodos es el de referencia (fig 1), es decir el nodo que va a tierra por lo tanto allí el voltaje es
0.
2. aplicando leyes de kirchhoff procedemos a plantear las ecuaciones para cada uno de los nodos; si el número de nodos es
n, el número de ecuaciones será
n − 1 porque siempre se escoge un nodo de referencia el cual no se le elabora ecuación.
3. Para hallar la ecuación de cualquier nodo, empezamos asumiendo una polaridad en cada resistencia, de acuerdo al nodo que vayamos a analizar.
4. Teniendo las ecuaciones planteadas, determinamos las variables matemáticas y se procede a resolver el sistema de ecuaciones por los diferentes métodos algebraicos
Ejemplo: Del siguiente circuito debemos hallar los voltajes en sus diferentes nodos
Si se quiere calcular el voltaje en el nodo Va, decimos que laresistencia de
2Ω tiene la siguiente
polaridad
 simplificando
simplificando
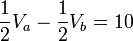 Para calcular el voltaje en el segundo nodo (Vb) las
Para calcular el voltaje en el segundo nodo (Vb) las resistencias que van a dicho nodo tendrán la siguiente polaridad
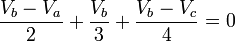 factorizando obtenemos
factorizando obtenemos
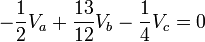 Para la polaridad del nodo Vc asumimos así:
Para la polaridad del nodo Vc asumimos así:
 factorizando obtenemos
factorizando obtenemos
 Obtenemos un sistema de ecuaciones del cual podemos determinar los
Obtenemos un sistema de ecuaciones del cual podemos determinar los valores del los voltajes en los nodos.
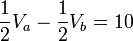
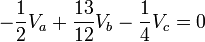
 obteniendo como resultado de los voltajes:
Va = 42.5V
Vb = 22.5V
Vc = 12.5V
obteniendo como resultado de los voltajes:
Va = 42.5V
Vb = 22.5V
Vc = 12.5V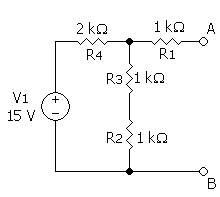

























 no puede acumularse en un nodo.
no puede acumularse en un nodo.