Metodos de las corrientes: Teorema de norton

Paso 1: El circuito original

Paso 2: Calculando la intensidad de salida equivalente al circuito actual

Paso 3: Calculando la resistencia equivalente al circuito actual

Paso 4: El circuito equivalente

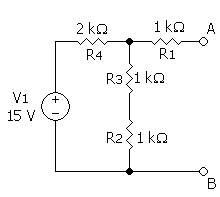
En el ejemplo, I_total viene dado por:

$I_\mathrm{total} = {15 \mathrm{V} \over 2\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega \| (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega)} = 5.625 \mathrm{mA}$

Usando la regla del divisor, la intensidad de corriente eléctrica tiene que ser:

$I = {1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega \over (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega)} \cdot I_\mathrm{total}$

$= 2/3 \cdot 5.625 \mathrm{mA} = 3.75 \mathrm{mA}$

Y la resistencia Norton equivalente sería:

$R = 1\,\mathrm{k}\Omega + 2\,\mathrm{k}\Omega \| (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega) = 2\,\mathrm{k}\Omega$

Por lo tanto, el circuito equivalente consiste en una fuente de intensidad de 3.75mA en paralelo con una resistencia de 2 kΩ

Metodos de las corrientes

jueves, 5 de mayo de 2011

Teorema de norton

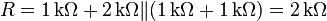
No hay comentarios:

Publicar un comentario